高校数学レベルで理解可能な内積の性質と、その利用法について簡単にまとめる。
定義
ベクトル $\vec{a} = (x_a, y_a)$ と $\vec{b} = (x_b, y_b)$ について、内積 $\vec{a} \cdot \vec{b} $ は以下の等式で定義される。
$$ \begin{equation} \label{inner-product} \vec{a} \cdot \vec{b} = x_a x_b + y_a y_b \end{equation} $$
主要な性質(余弦定理との関係)
内積の主要な性質として、以下の等式が成立することが知られている。
$$ \begin{equation} \label{inner-product-cos-thm} \vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos \theta \end{equation} $$
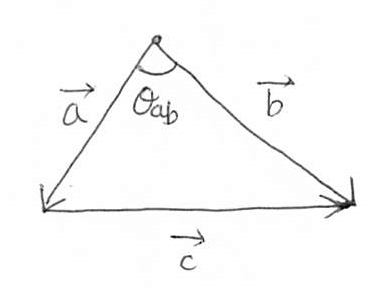
このことは、ベクトル $\vec{a}$ と $\vec{b}$ によって張られる三角形を考えて、余弦定理 $c^2 = a^2 + b^2 - 2ab \cos \theta_{ab}$ を変形して得られる等式
$$ \begin{equation} \label{inner-product-alt} |\vec{a}||\vec{b}| \cos \theta_{ab} = \frac{|\vec{a}|^2 + |\vec{b}|^2 - |\vec{c}|^2}{2} \end{equation} $$
の右辺を実際に計算することで確かめられる。ただし、 $\vec{c} = \vec{b} - \vec{a} = (x_b - x_a, \ y_b - y_a)$ である。
練習問題:式 $\ref{inner-product-alt}$ の右辺を実際に計算し、 式 $\ref{inner-product}$ と一致することを確かめよ。
内積の値そのものを目に見えるように図示することは難しいが、式 $\ref{inner-product-cos-thm}$ によって $\cos \theta$ の値を計算できるため、便利な利用方法がいくつか存在する。
直交判定
$\cos (\pi/2) = 0$ であるから、$\vec{a}$ と $\vec{b}$ が直交している場合、式 \ref{inner-product-cos-thm} より $\vec{a} \cdot \vec{b} = 0$ となる。つまり、ベクトル $\vec{a}$ と $\vec{b}$ の成分さえ分かっていれば、簡単な掛け算と足し算だけで直交しているかどうかの判定ができる。
練習問題:
- $\vec{a} = (12, \ 4)$ と $\vec{b} = (-3, 9)$ が直交していることを確かめよ。 また、$\vec{c} = 4\vec{a} = (48, 16)$ と $\vec{b}$ ではどうか。
- 自分で適当に2ベクトルを定め、直交しているかどうかを判定せよ。
三角形の面積
ベクトル $\vec{a}$ と $\vec{b}$ で張られる三角形OABの面積を求めることを考える。
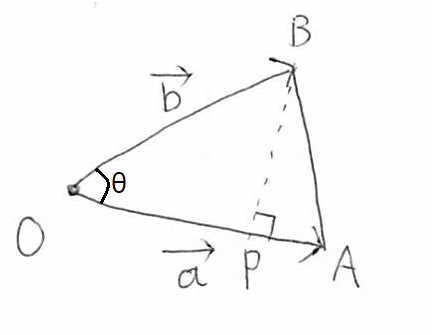
三角形の面積は (底辺×高さ)/2 で求められるから、点Bから $\vec{a}$ に下した垂線の長さを知りたい。 ここで、垂線の足をPとして直角三角形OBPを考えると、垂線BPの長さは $|\vec{b}| \sin \theta$ であることが分かる。
三角関数の関係式より $(\sin \theta)^2 + (\cos \theta)^2 = 1$ であるから、 $\sin \theta = \pm \sqrt{1 - (\cos \theta)^2}$ である。本当なら $\sin \theta$ の符号を真面目に考える必要があるのだが、面積を求める上では最後に絶対値を取れば無視できるので、とりあえず非負(正か0)であると思うことにする。このとき、三角形の面積は以下のように書くことができる。
$$ \begin{equation} \label{triangle-area} \triangle OAB = \frac{|\vec{a}||\vec{b}| \sin \theta}{2} = \frac{|\vec{a}||\vec{b}|\sqrt{1 - (\cos \theta)^2}}{2} \end{equation} $$
辺aとbの長さしか分かっていないのなら$\cos \theta$を求める方法は存在しないが、今はそれぞれの辺が$\vec{a} = (x_a, y_a)$と$\vec{b} = (x_b, y_b)$と表されることが分かっている。ここで2ベクトルの内積を取ると、式 $\ref{inner-product-cos-thm}$ によって、$\cos \theta$に辺aとbの長さを掛けたものが得られる。aとbの長さは分かっているので、結局$\cos \theta$そのものの値を得ることができて、式$\ref{triangle-area}$に代入すると面積を求められる。
練習問題:
- 式 \ref{inner-product-cos-thm} を用いて、$\cos \theta$ を $\vec{a}$と$\vec{b}$の式として表せ。
- 得られた $\cos \theta$ の式を式 \ref{triangle-area} に代入し、外側の$|\vec{a}||\vec{b}|$を用いて根号内の分母を払え。
- 得られた式に含まれるベクトルを展開して、$\triangle OAB$を $x_a, y_a, x_b, y_b$ の式で表せ。
内積と外積
先ほどの練習問題を最後まで計算すると $$ \triangle OAB = \frac{x_a y_b - y_a x_b}{2} $$
という形の式が得られる。実は右辺の分子 $x_a y_b - y_a x_b$ には外積という名前がついており、$\vec{a} \times \vec{b}$ で表す。 厳密には外積 $\vec{a} \times \vec{b}$ の値は3次元ベクトルとして定義され、そのベクトルは$\vec{a}$ と $\vec{b}$ の両方に直交し、長さは $\vec{a}$ と $\vec{b}$ の張る平行四辺形の面積に等しい。$\vec{a}$ と $\vec{b}$ がどちらもXY平面上にある場合は、この平面に直交する向きはZ軸と平行になるため $\vec{a} \times \vec{b} = (0, \ 0, \ x_a y_b - y_a x_b)$ であり、この時のZ成分も便宜的に外積と呼ぶことがあるのである。
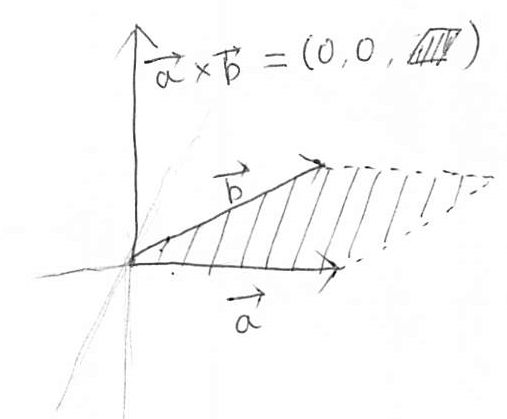
ここまでの流れから気付くかもしれないが、外積$\vec{a} \times \vec{b}$は$|\vec{a}||\vec{b}|\sin \theta$に等しい。定義式の形も内積となんとなく似ているが、こちらの関係はより内積との対応関係を感じさせるものになっている。
外積は定義式に引き算を含むことや、図形的な等式に$\sin \theta$を含むことから推察されるように、$\vec{a}$と$\vec{b}$の順番をひっくり返すと正負が逆転する。すなわち、$\vec{a} \times \vec{b} = -(\vec{b} \times \vec{a})$である。図形的には外積の結果として出てくるベクトルの向きに影響するが、この関係は俗に「右ねじの進む向き」と呼ばれる。$\vec{a}$から$\vec{b}$に回すのと同じ向きで右ねじ(いわゆる普通のねじ)を回すと、$\vec{a} \times \vec{b}$ベクトルの向きにねじが進むという意味である。
外積の値は平行四辺形の面積になり、2で割ると三角形の面積になるという事実は、覚えておくとたまに役に立つことがある。
コサイン類似度
$\cos \theta$ は円周上の点のX成分の大きさだから、$\theta = 0$ で最大値 $\cos \theta = 1$ を取り、$\theta = \pi$ で最小値 $\cos \theta = -1$ を取る。したがって、一方のベクトルをX軸正の方向に固定して、もう一方のベクトルを反時計回りに回転させていくと、2つのベクトルがだいたい同じ向きを向いているときには $\cos \theta$ は1に近い値を取っているが、直角に近づくにつれて値は0へと近づいていき、逆方向を向き始めると更に小さくなって負になる。
$\cos \theta$ のこの性質を利用しているのが コサイン類似度 と呼ばれるものであり、現実での内積の利用法の一つである。これは大雑把に言うと、2つのベクトルがどれくらい似ているかどうかを測るための尺度の一つである。
ベクトルという概念は平面上の点を表すためだけのものではなく、一般的に複数の数値の列として表されるものはだいたいベクトル表記ができる。
- 例:コンピュータ上で色を扱うときにはR, G, Bという光の三原色の配分で色を表すが、この3要素からなる $(R, G, B)$ は色を表すベクトルである。たとえば、$(R, G, B) = (255, 128, 0)$ というベクトルはオレンジ色を表す。言い換えると、3次元空間の点 $(255, 128, 0)$ をRGBの色として解釈するとオレンジ色になる。
- 例:味覚は甘味、酸味、塩味、苦味、うま味という基本味の組み合わせからなるとされているが、それぞれの基本味の強さを数値で表したとき(たとえば0~10とする)、5つの数値を組にしてベクトルを作ることができる。このベクトルは5次元空間の点を表すものでもあり、特定の味を表すものでもある。
このようにして概念をベクトル化したとき、ベクトル同士がどれくらい似ているかを評価できると便利である。たとえば $(255, 128, 0)$ のオレンジ色と $(230, 130, 50)$ の黄土色は似ているが、$(255, 0, 128)$ のピンク色とはあまり似ていない。ベクトルの各成分さえ分かっていれば、式 $\ref{inner-product-cos-thm}$ を利用することで簡単に $\cos \theta$ が求められるため、「似ている度」を測る簡易な指標として使うことができる。
練習問題:例に挙げた色どうしで $\cos \theta$ の値を求め、自分の感覚と比較してみよ。
複数の値を一つの値に押し込めてしまう都合上、コサイン類似度は万能の概念ではない(これはコサイン類似度に限った話ではなく、何かを計測するという行為一般に常について回る問題である)。色の例で言えば、白 $(255, 255, 255)$ と灰色 $(128, 128, 128)$ のコサイン類似度は1であるが、白と灰色が同じであると言う人はまずいないだろう。評価指標は目的に応じて適切に作る必要がある。